Long term interest rates, as captured by the yield on long term US Treasury Bonds, have recently swung upwards after falling for three decades. It’s still too soon to say that the long bull market in bonds has ended, because rates could fall again, but yields are at historically low levels still so the scope for further reductions is limited (see chart below).
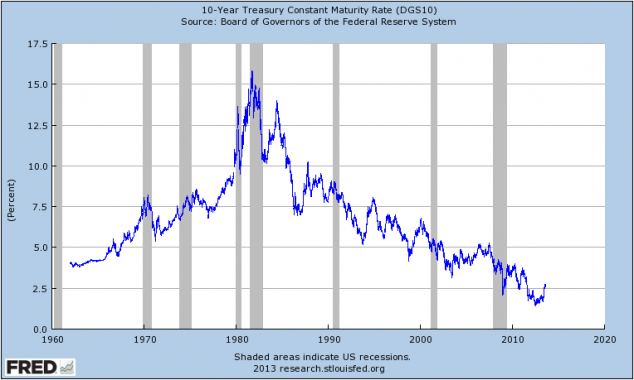
Note how the recent “surge” in bond yields merely took them back to where they were two years ago, and they remainar below the average since the 1960s.
The rise in yields was triggered by Ben Bernanke’s comments Congress in May on the timing of the ending of quantitative easing, a policy in which the Fed, having exhausted its scope for cutting short term interest rates, buys financial assets such as government bonds and mortgage backed securities, to push down longer term interest rates. With the US economy tentatively improving (though job creation remains weak for this stage of the recovery) the Fed expects to start “tapering” off its bond purchases as soon as this autumn, though it indicates that short term rates will remain very low for some time after that, probably into 2015.
The rise in long term interest rates can be decomposed into the a change in expected short term rates and a “term premium”. The conventional (“unbiased expectations hypothesis“) economic theory of interest rates determination says that long term interest rates should be the same as what you would get by holding a sequence of short term interest rate assets reinvesting the proceeds of each maturing short term bond in the next one. If this is not the case then there would be an arbitrage opportunity (*) and the market would be out of equilibrium.
But that is not the whole story. Holders of longer term assets face the possibility that interest rates will change in the future and this risk needs to be compensated. So, on top of the compounded effect of expected short term rates, there is a term premium, an additional amount of interest that investors require to be willing to hold long term bonds. Theoretically the term premium could be negative – long term investors such as pension funds and life insurance companies value the ability to buy long term assets which provide a cashflow match to their long term liabilities. But in practice it is normally positive.
The term premium cannot be directly observed. In this respect it is like its cousin the equity risk premium (ERP), which is the extra expected return that investors require for holding equities as an asset class compared with government bonds, which are less risky. The ERP is often described as the most problematic number in finance because: i) it is impossible to measure directly; and ii) estimates of its scale are hard to reconcile with the economic model of risk aversion that underpins the whole of asset pricing theory.
The term premium is less important and problematic than the ERP but it is still something of a puzzle. There are various ways of measuring it, which produce somewhat different estimates, rather like the ERP. You can estimate it econometrically and there are several different approaches, some based on a fundamental model of risk aversion and others based on a statistical analysis of what seems to be actually driving interest rates. Or you can ask investors directly. Here is a chart from a 2007 Federal Reserve Board of San Francisco paper which shows the results from four ways of estimating the term premium.
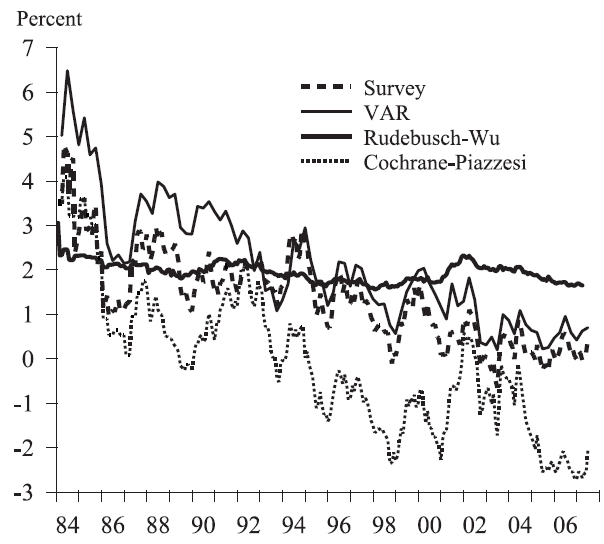
VAR here means vector autoregression (NOT value at risk) which is a statistical technique for extracting information from time series. The VAR method estimates market expectations of short term interest rates into the future and the compares these with the actual long term rate to capture the difference, which is the term premium. Cochrane-Piazzesi is a purely empirical method of estimating expected long term rates . Rudesbusch-Wu is derived from a macroeconomic model which includes variables such as the expected rate of inflation, which plausibly varies over time, and particularly so in the 1980s and 1990s.
Although all four methods show a downward trend over the period, the magnitude varies considerably. With long term interest rates recently in the 2-3% range, a margin of error of 1-2 percentage points is very large.
But economists need to understand what is driving market interest rates so they keep estimating the term premium. The New York branch of the Federal Reserve recently did an estimated decomposition of the rise in long rates between changes in expected short rates and the term premium. Their findings, reported here, show that most of the rise was due to rising term premia. (The FRBNY authors use yet another econometric method of estimating the term premium, explained in this paper.)
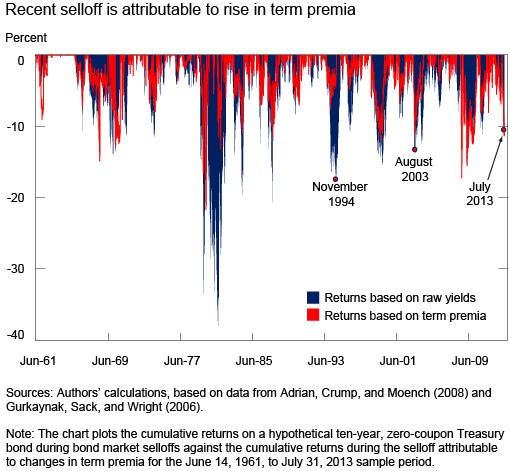
The FRBNY report also shows that the recent bond sell off is large but not extraordinary by historical standards. The fact that the rise in rates is driven by a change in term premia means that it is not that investors expect a different path of short term interest rates from what they expected before. The unwinding of the Fed’s bond purchases is instead causing a reappraisal of the inherent risk of holding long term bonds. But the volatility of that term premium and the difficulty of estimating it accurately complicate the Fed’s decisions on monetary policy.
A leading City economist told me recently that in his opinion the market reaction to Bernanke’s speech was investors pricing in the sheer uncertainty of the exit from QE, which has never been done before. The Fed has consistently emphasised that although it will take all possible steps to exit QE in an orderly way, there are uncertainties about this stage of policy, just as there were uncertainties about the effect of QE in the first place (and still are, as we don’t know for sure what would have happened without QE).
Market commentary on the term premium can be a little over-confident and often glosses over the imprecision of any estimates. For example this recent article on Bloomberg quotes a report on the term premium as if it were a straightforward matter to calculate it. The Fed is much less confident and has to cope with the knowledge that its model of how investors behave is subject to a large margin of error.
*
(*) Consider a very simple example. There is a 1 year bond that has an interest rate (or more accurately a yield to maturity, which takes into account the time value of the cashflows received – it’s the internal rate of return of the bond) of 5% now and a market expected interest rate of 6% in the second year. If you buy the bond and reinvest the proceeds after one year in another one year bond then you expect to get the product of 5% and 6% which is 11.3%. If there is also a 2 year bond trading in the market and it has an interest rate of more than 11.3% then you would sell the short term bond (go short) and buy the long bond, because you can in effect borrow at 11.3% and invest at more than 11.3%. Equally, if the long bond interest rate was less than that of the compounded short bonds rates, then it would make sense to do the opposite. Only when the expected rates of return are equal is there equilibrium in the market.
This example assumes: i) zero transactions costs; and ii) bonds of differing maturity being otherwise identical from the point of view of investors. Transactions costs in the US Treasury bond market are very low indeed. But the second condition is broken by the risk associated with holding longer bonds, which is compensated for by the term premium.


Joanne Tay
Thank you for this.
Everett Brown
Very good review.