Introduction
Conventional finance theory is based on the microeconomic theory of consumer choice under uncertainty. This is a long established theory with some serious weaknesses. On the MFin we have a core course called “Economic foundations of finance” which shows where finance theory comes from and, in passing, should make students a bit more cautious about applying that theory.
Rational economic agents
The starting point is the idea of a rational consumer. Economists use the word rational in a limited and particular sense. To an economist a rational person is one who knows what she wants in all possible situations. Faced with a near infinite range of choices over what to buy and how to spend one’s time, the rational consumer knows; she is never halted by indecision. This is captured technically by the idea of a complete preference ordering. An ordering is a ranking, or a method of putting choices in a particular order. Faced with apples, pears and bananas in the shop, the rational consumer knows which she prefers. She can rank, or order, the three options. Economists are unconcerned with how she does this or where her preferences come from, it matters only that she can make the choice. So there is never a situation where she is stumped and doesn’t know what she wants.
A person may have strange, antisocial or self-destructive preferences (for drugs for example, or trying to rule the world) but economists choose not to comment on the content of people’s preferences. They just insist that rational economic agents have a full set of preferences.
Second, she is rational in the sense that her choices are consistent. She does not have preferences that lead to paradoxical choices. If she prefers apples to bananas and bananas to pears, then she must, if she is rational, prefer apples to pears. That is, her preferences are transitive. On different days she may have different preferences, so perhaps she prefers pears on a hot day or just on Thursdays, but she may not prefer apples to bananas, bananas to pears and pears to apples at the same time – that would be irrational.
Indifference curves
The expression of preferences is done either graphically or mathematically. The graphical approach, which is limited to preferences over two choices, is known as an indifference curve, invented in the early 20th century by Vilfredo Pareto, who is associated with the important concept of pareto efficiency in welfare economics and the pareto distribution in statistics. Here is a set of indifference curves (an indifference map):
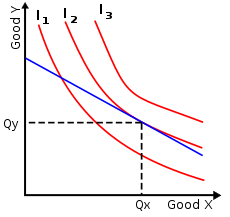
Taken from Wikipedia, this shows indifference curves for a consumer, over two goods, x and y. The lines I1, I2 and I3 describe combinations of the two goods which are equally preferred by the consumer. Older economic textbooks expressed this as saying that the consumer had equal utility along an indifference curve. “Utility” expresses the desirability of goods and services. Early economists thought it might be possible to actually measure utility and quantify it. But modern economics treats that as a futile and unnecessary task. You can think of an indifference curve as showing combinations of goods that provide the same utility or you can regard them as equally preferred combinations, the meaning is the same.
This little diagram tells us more about what economists routinely assume about rational people. First, the further the indifference curve lies away from the origin, the more preferred are the combinations. So I3 represents combinations that are better (more preferred) than I2 or I1. The curves are like contours on a map, where the ground is rising upwards and to the right. Why? Because it is assumed that people are greedy, they would always prefer more to less. Technically it’s known as non-satiation of wants, but greedy is pretty accurate. Our rational consumer will always choice the highest indifference curve she can reach. Her choice is constrained in practice by her income, or her budget constraint, which can be shown as a downward sloping straight line joining the two axes like this:
The blue budget line constrains the consumer. It is derived by dividing her income by the price of good y (which marks the left hand extreme point of the line, where she buys only good y) and doing the same with the price of x (which defines the right hand extreme point where she buys only good x). The two points are then joined by a straight line, representing all the feasible combinations of goods x and y she can buy. She will choose the highest indifference curve compatible with her income/budget. In this case it’s I2. She would prefer I3 but hasn’t got enough money to pay for it. I1 is affordable but inferior to I2, so she would never rationally choose it.
The second thing to notice is the shape of the indifference curves. They are downward sloping and convex with respect to the origin. The downward (negative) slope reflects non-satiation – more is preferred to less so indifference curves can’t slope upwards. The curved shape (the convexity, the falling absolute slope of the curve) reflects another assumption about rational people: they prefer combinations of things more than just having a lot of a single thing. The psychological idea is that as you have more of something, the marginal contribution it makes to your utility (happiness, satisfaction) diminishes. This is therefore known as diminishing marginal utility. You would always prefer more than less, because we just assumed you’re greedy. But if you’ve got ten bananas already, the eleventh banana gives you less utility than the tenth. That means that, if you like bananas and apples, at that point you would probably value a single apple more than another banana. More generally you will choose/prefer more equal combinations of both to options that provide a lot of one and hardly any of the other.
The best way to get comfortable with indifference curves is to draw different shapes from those above and see how they imply behaviour at odds with the rational agent assumptions. For example, imagine an indifference curve that was a horizontal line at the number 1 on the y axis, where good y is bananas and good x is pears. That would imply the consumer was equally happy (equally preferred, got equal utility) from having one banana and two pears or one banana and three pears or one banana and four pears and so on. But if more is always preferred to less that can’t be right. The curve must have downward slope.
Utility functions
The information contained in indifference curves can also be captured in a utility function, which is an equation that expresses the information about the consumer’s preferences. Utility functions are easily generalised to many goods and services, while indifference curves can stretch to three at most before we run out of dimensions. This is an example of a commonly used function in economics teaching, known as Cobb-Douglas:
U = XβY (1−β)
The Cobb-Douglas form says utility is a weighted exponential average of the amount of the two goods concerned. There is no meaning in the quantity of utility, we simply require that more utility corresponds to a more preferred set of goods. This equation is for just two goods x and y and can be translated into an indifference curve. An indifference curve is an equation along which utility is constant, by definition. The total differential of this equation is:
dU =∂U/∂X*dX +∂U/∂Y*dY
where ∂U/∂X is the partial derivative of U with respect to X, the amount by which utility changes when the amount of good X consumed changes. dU is the total change in utility. By definition this is zero on an indifference curve, so the expression is set equal to zero. The two partial derivatives can be calculated quite easily (that’s why the Cobb-Douglas form is so popular) and you end up with this equation for the slope of the indifference curve:
dY/dX = −βUY/(1 − β)UX = − βY/(1 − β)X
Once you substitute actual numbers for Y, X and β you can plot the indifference curve. Note that the slope is negative (assuming β is positive), consistent with the economic assumption of greediness.
If your multivariate calculus is a bit rusty, this might seem slightly daunting but the important thing to know is that indifference curves and utility functions are equivalent ways of capturing information about preferences. Indifference curves are easier for learning the concepts but equations are far more flexible.
The assumption that indifference curves and the utility functions they represent are convex means that we can use the tools of convex optimisation theory to predict what consumers will do, including when faced by changes to prices and incomes. Normally life is made easier still by assuming that the curves are smooth and the equations are differentiable, so you can use the Lagrangian methods of calculus, as will be familar to economics students. But the theory depends on convexity not on differentiability.
From economics to finance
So what is the significance of all this for finance? The goods x and y can be thought of very generally, including as risk and return. Returns are a good thing (positive utility, more is preferred to less) whereas risk is usually a bad thing (less is preferred to more, or equivalently certainty, the absence of risk, is a positively preferred thing). So we can construct an indifference curve that shows economic agents preferring different combinations of risk (or the absence of risk – certainty) and return. The basic derivation of portfolio theory and then of the capital asset pricing model builds on this idea, that investors trade off risk against return. Risk is measured in economics by the variance (or its square root, the standard deviation) of the returns on an asset. The return is the average (mean) return on the asset. So a great deal of finance comes down to the mean-variance optimisation model, as introduced by Harry Markowitz and James Tobin in the 1950s. The risk free rate is a return you can get with absolutely no risk. At the other extreme you can find the highest return asset, but with a lot of risk. Depending on the level of risk aversion (or risk appetite, tolerance) the consumer will choose a portfolio with some combination of risky and risk-free assets. Modern portfolio theory (now sixty years old) explains how this turns into a much more tractable problem once we introduce the benefits of diversification.
Most of the assumptions made by economists have been challenged. That doesn’t invalidate them, the question is whether the theory they support has value in explaining and predicting actual behaviour. The most important challenge comes from behavioural economics, rooted in experimental psychology, which suggests that where risk is concerned, the model is quite often wrong; people, even very intelligent ones, often do not make “rational” decisions when faced with risk. Behavioural finance is now an accepted adjunct to mainstream finance theory but attempts to use it either to predict behaviour or to invest (by exploiting the irrationality of others) have not yet been very successful. The best single guide to a practical application of behavioural finance is Robert Shiller’s extremely readable “Irrational Exuberance”. Get the second edition, as it covers the US housing bubble, in addtion to the dot com bubble of the late 1990s.
Further reading
Wikipedia is pretty good on these subjects, though each topic tends to span the basic and the more complex, so ignore the latter. The topics consumer choice, indifference curve and preferences all are quite self contained and have many links to related topics. There are lots of other resources online on these topics. Here is a good one on indifference curves for example.



Leave a Reply